| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 횡스크롤
- 헌법재판소
- 부산광역시
- 네트워크
- 지금다시헌법
- 고통에
- 응답하는
- 정책
- 공부
- 공간밀도
- 과학의과학
- 점프
- 헌법
- 파이게임
- 사회
- 파이썬
- 맵
- 지금 다시
- Latent Dirichlet Allocation
- 타인의
- 주요일간지
- 파이썬 기초
- 연구하며
- 정치
- 사법부
- LDA
- pygame
- 사법
- python
- 글쓰기
- Today
- Total
RoNS 님의 블로그
[cities] 공간상에 점들의 패턴을 파악해보자! 본문
시각화로 이해하는 점 분포 패턴과 Ripley’s K 함수
우리 주변의 공간은 사실 수많은 점들로 이뤄져 있습니다.
건물의 위치, 사람의 거주지까지—이 모든 것을 ‘점’으로 표현할 수 있다면,
이 점들이 공간상에서 어떤 방식으로 퍼져 있는지 분석하는 것은 어떤 의미가 있을까요?
이번 글에서는 공간의 점 분포 패턴을 이해하고, 이를 시각적으로 표현하고 해석하는 방법을 소개합니다.
특히 Ripley’s K 함수와 L 함수를 중심으로, 실제 분석에서 사용되는 기법과 그래픽을 통해 쉽게 풀어보겠습니다.
✅ 점 분포 분석이 중요한 이유
도시계획, 생태학, 사회문제 분석 등 다양한 분야에서 우리는 “어디에 무엇이 집중되어 있는가?”라는
질문을 던집니다. 점 분포 분석은 이를 과학적으로 해석하는 방법입니다.
대표적인 분석 요소는 다음과 같습니다:
거리(Distance): 점과 점 사이의 물리적 간격
근접성(Adjacency): 가까운 점들의 분포 경향
군집성(Clustering): 특정 위치에 점이 몰려 있는 정도
규칙성(Regularity): 점들이 얼마나 일정한 패턴을 이루는지
🔍 점 분포 유형 살펴보기
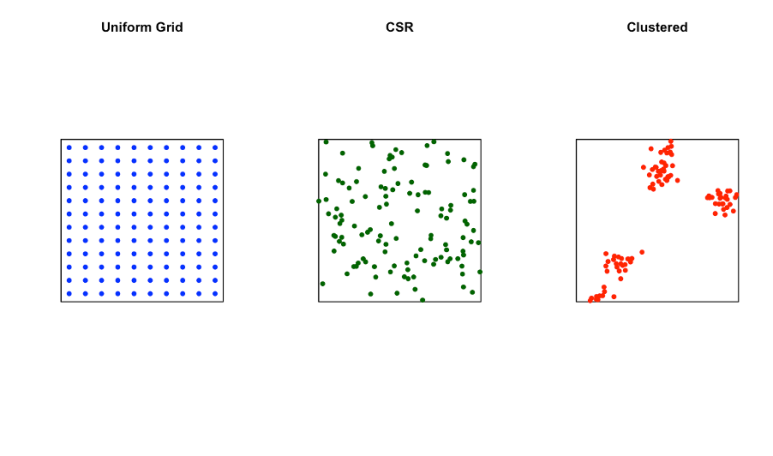
아래 이미지는 공간상에서 점이 어떤 방식으로 배치될 수 있는지를 보여줍니다.
Uniform Grid: 격자처럼 규칙적으로 배치된 점 (파란색)
CSR (Complete Spatial Randomness): 완전 무작위한 분포 (녹색)
Clustered: 특정 영역에 점이 집중된 분포 (빨간색)
각 패턴은 서로 다른 공간 현상을 반영합니다. 예를 들어 군집 분포는 상권, 생물 군락지, 혹은 범죄 발생 지역과 같은 집중된 활동을 의미할 수 있습니다.
📐 최근접 이웃 분석: 가장 가까운 친구는 누구?
가장 직관적인 분석은 각 점에서 가장 가까운 다른 점까지의 거리를 측정하는 것입니다. 이를 ‘최근접 이웃(Nearest Neighbor)’ 분석이라고 합니다.
위 그림에서 파란 선은 각 점과 가장 가까운 점을 연결한 것입니다.
점이 고르게 분포되어 있다면 선의 길이도 일정하게 나타납니다. 반면 군집이 있을 경우, 특정 지역의 선들이 짧게 뭉쳐 나타나게 됩니다.

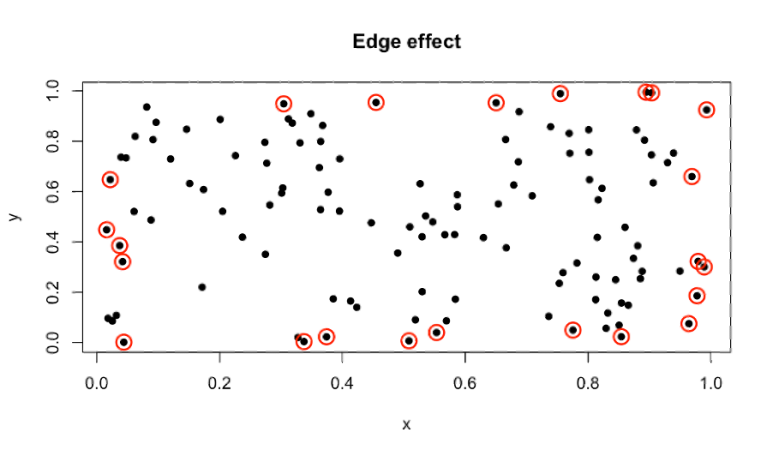
🚧 경계 효과(Edge Effect)는 왜 중요할까?
현실 세계에는 분석 가능한 공간에 경계가 존재합니다.
경계 근처의 점은 이웃 점을 찾을 수 있는 방향이 제한되기 때문에 분석이 왜곡될 수 있는데,
이를 Edge Effect라고 부릅니다.
위 그림에서 빨간 원은 Edge Effect가 발생할 수 있는 점을 표시합니다.
이러한 점들을 고려하지 않으면 평균 거리나 밀도 분석 결과가 왜곡될 수 있으므로, 보정이 필요합니다.
📊 Ripley’s K 함수와 L 함수로 분포를 정량적으로 측정해보자
단순히 눈으로 보는 것보다 더 정밀한 분석이 필요할 때 사용하는 것이 바로 Ripley’s K 함수와 L 함수입니다.
**K 함수(K(r))**는 반경 r 안에 포함된 점의 수를 누적적으로 분석
**L 함수(L(r))**는 K 함수의 선형화된 형태로 해석이 쉬움
🔬 각 패턴별 분석 결과는 다음과 같습니다:
왼쪽: 규칙적 분포 → 관측선이 기준선 아래
가운데: 무작위 분포 → 관측선이 기준선과 일치
오른쪽: 군집 분포 → 관측선이 기준선보다 위
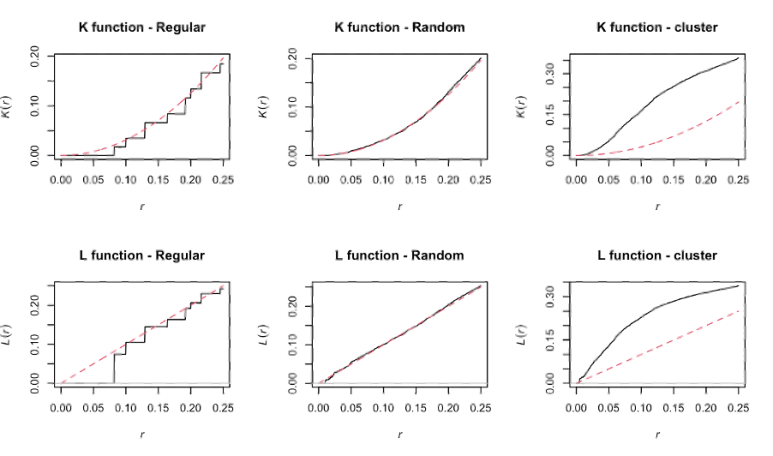
해석 팁:
관측선이 기준선(붉은 점선)을 초과하면 군집 경향
기준선 아래이면 규칙적 구조
거의 일치하면 무작위 분포
🧭 마무리하며: 점은 단순한 점이 아니다
단순히 점이 어디에 있느냐가 아니라,
그들이 어떤 패턴을 이루며 퍼져 있는지, 서로 어떤 관계를 갖는지를 파악하는 것이 분석입니다.
이러한 점 분포 분석은 다음과 같은 적용될 수 있습니다:
도시 내 상권 분석, 범죄 발생지 군집 탐색, 생태 군락지 분포 파악, 도보 접근성 분석 등 그래도 연구를 할 때는 흥미를 느낄 수 있는 주제를 가지고 연구해야겠죠?ㅎㅎ
다음 주에는 방격 분석과 거리 기반의 검정 방법을 리뷰해 보겠습니다!
'Cities' 카테고리의 다른 글
| [cities] 방격분석(Quadrat Analysis)을 활용한 공간점 분포 검정 (0) | 2025.06.14 |
|---|---|
| [Cities] Kernel Density를 활용한 공간 밀도 시각화 (0) | 2025.05.27 |
| [Cities] 공간 밀도 추정(Kernel Density) 쉽게 이해하기 (0) | 2025.05.22 |
| [Cities]📍 R로 공간정보 불러오기부터 인구 정규성 검정까지! (2) | 2025.05.16 |
| [Cities]지리공간정보의 그래프와 기초분석 : GIS의 시작점(3) (0) | 2025.05.08 |





